If you like to tinker with maths and are looking for more exotic operators, for example to calculate the Factorial or the Fibonacci series, then this is something you are going to have to implement yourself in LiveCode. But there is no need to despair, this can be done pretty much with a single line, wrapped in a function definition.
MATHS HAZARD – You may skip the following paragraph if you are not a friend of mathematical definitions.
The Factorial of a non-negative number n can be defined as the product of all of its positive integers that are less than or equal to n, with the Factorial of 0 returning 1. The operator for Factorial is denoted by an exclamation mark (!), allowing us to write the operation as follows: n!
The following example demonstrates how Factorial is calculated for the number 6:
6! = 1*2*3*4*5*6 = 720
Now this does not seem to be too much of an issue to implement or write, but how do you go about writing a function in LiveCode that does all the heavy lifting for you, so that you do not have to write a long sequence of multiplications?
Well, there are fundamentally two algorithmic approaches you could consider. These are iteration and recursion. They both operate in quite different ways and have advantages and disadvantages.
Let us look at the iterative approach first, as this is possibly the programming paradigm most people are familiar with.
We create a function that takes an argument for which we are calculating the Factorial product. This function then cycles through all the positive integers that are less than or equal to the initial argument and multiplies all of these integers together. The function result is the Factorial result.
function factI x local tProduct = 1 local tCounter repeat with tCounter = 1 to x multiply tProduct by tCounter end repeat return tProduct end factI
Now in order to implement this algorithm we need two local variables and a repeat loop. This keeps track of the result as it is being updated through each iteration of the loop. But what if you really do not want to be bothered with local variables and loops and keeping track of data?
Well, meet recursion. Recursion can remember all the data that is specific to an instance of a function call. This means that we can pretty much throw most of the code away that we use in the iterative approach. Yes, we do not need local variables and we do not need a repeat loop. In fact, we can calculate the Factorial of a number with a single line of code in a function.
A recursive implementation usually contains some kind of condition check so it knows when to stop and when to call itself. This has been implemented in the following code using an “if then else statement”. If we are below a certain value stop, otherwise call the function again, but with a changed argument.
function factR x if x < 2 then return 1 else return factR (x - 1) * x end factR
Now that was not too painful, but what is actually going on here that allows us to write code that is so much shorter?
Consider calculating 6! and let us expand how factR calls itself at each recursive level:
Level 1: factR(6) Level 2: (factR(5) * 6) Level 3: ((factR(4) * 5) * 6) Level 4: (((factR(3) * 4) * 5) * 6) Level 5: ((((factR(2) * 3) * 4) * 5) * 6) Level 6: (((((factR(1) * 2) * 3) * 4) * 5) * 6) (((((1 * 2) * 3) * 4) * 5) * 6) = 720
Note: The parentheses demonstrate the execution order at each level and are not intended to be interpreted in a mathematical sense. The commutative law applies.
So this gives us a total of 6 calls to the function factR for 6!
Another number sequence we mentioned in the beginning is that of Fibonacci. This sequence received its name from Leonardo of Pisa who published the historical mathematics book “Liber Abaci” around 1202. Leonardo of Pisa was also know by the name Fibonacci.
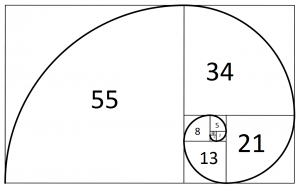
This Fibonacci number sequence starts: 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,. . .
This sequence has fascinated mathematicians for centuries and reveals remarkable patterns that are very much linked to natural structures, such as the formation of shells, branches and even the arrangement of the seeds in sunflowers. My particular interest is the use of the Fibonacci numbers for the close approximation of the Golden Ratio.
A Fibonacci number is generated by calculating the sum of the previous two numbers in the Fibonacci sequence. This operation is quite different to that used to derive the Factorial number sequence, never the less, it is possible to also wrap this into an iterative and recursive implementation.
Calculating the Fibonacci numbers iteratively requires additional local variables, compared to calculating the Factorial numbers. We step through all of the Fibonacci numbers and create the next ones by adding the previous two numbers together.
function fibI x local tFirst = 1, tSecond = 1 local tCounter, tSum repeat with tCounter = 3 to x put tFirst + tSecond into tSum put tSecond into tFirst put tSum into tSecond end repeat return tSecond end fibI
In order to implement this algorithm we need four local variables and a repeat loop. As with the Factorial calculation, this keeps track of the result as it is being updated through each iteration of the loop.
The recursive approach can again do away with local variables and the repeat loop, creating the implementation as follows:
function fibR x if x < 3 then return 1 else return fibR (x-1) + fibR (x-2) end fibR
Now I am not going to demonstrate how the recursive levels are expanded here and would like to leave this for the reader to explore. What I would like to add is that calculating the Fibonacci number for 6 calls fibR a total of 15 times.
Now recursion (or meta programming as it is sometimes referred to) is great as it can really reduce your code and hide a lot of the complexity, but beware. Some algorithms are better suited to recursion than others, and recursion can be computationally more expensive than iterative approaches. For example, calculating 20! calls factR 20 times, and that is great. Calculating the Fibonacci number of 20 calls fibR a staggering 13529 times.

15 comments
Join the conversationRicky Phillips - October 16, 2014
Ricky Phillips liked this on Facebook.
Stephan Uijthoven - October 16, 2014
Stephan Uijthoven liked this on Facebook.
Alan Stenhouse - October 16, 2014
Alan Stenhouse liked this on Facebook.
Mark Schonewille - October 16, 2014
Mark Schonewille liked this on Facebook.
Nicholas Westbury - October 16, 2014
Nicholas Westbury liked this on Facebook.
Seth Mould - October 17, 2014
The index entry in your User Manual says:
Recursion
…………………. see Recursion
which is not helpful. However, you have an awesome product guys! 😎
Seth Mould - October 17, 2014
Seth Mould liked this on Facebook.
jojohernandez - October 21, 2014
RT @runrev: Recursion for Runaways: If you like to tinker with maths and are looking for more exotic operators, for exa… http://t.co/XPX…
MaxV - October 21, 2014
Dear Hanson,
in this particular case recursion is not a good way. The code simpler and more correct to face Fibonacci sequence is using array. Arrays permit to construct the sequence without using local variables. Local variables in Livecode is bad programming to my humble opinion.
Here is the code:
function fibonacci n
if n <= 2 then
return 1
else
put 1 into fib[1]
put 1 into fib[2]
repeat with t=3 to n
put fib[t-1] + fib[t-2] into fib[t]
end repeat
return fib[n]
end if
end fibonacci
MaxV - October 21, 2014
Sorry, I misunderstood the sense of your post. English is not my first language.
I still don’t understand what is better between a repeat loop and an recursive function.
What are benefits and lacks of the two way?
Hanson - October 22, 2014
Hi Max,
thank you very much for posting your comments.
Indeed, the Fibonacci numbers do not lend themselves very well to being calculated in a recursive fashion, as demonstrated here. With this blog I was trying to show that there are alternative ways to solving a problem, focussing particularly on iterative and recursive approaches.
I would not say that there is a clear benefit for either recursion or repeat loops. It really depends on the problem you are trying to solve. That is what I tried to show by using two problems that have different computational complexities.
I like your implementation of calculating the Fibonacci numbers very much. This approach can return the the entire sequence up to n if you return the complete array. As a mind experiment this could probably also be implemented in a recursive fashion, although personally, I would stick with your implementation.
MaxV - October 22, 2014
Hi Hanson,
did you try to calculate the Fibonacci of 1476? Recursion way get too much time…
However with Fibonacci of 1477 or more I get “1.#INF”. Is it normal?
Hanson - October 23, 2014
Hi Max,
the computational complexity of calculating the Fibonacci number recursively is exponential, so trying to calculate the Fibonacci number for 1476 recursively would take an incredibly long time, but you would probably hit time or resource limit before the calculation ever came to an end.
With regards to “1.#INF” in the iterative approach, this indicates that you have overflowed the numerical representation limit in LiveCode. I would expect to see this kind of computation exception with the size of numbers you are trying to calculate here.
I forgot the name - November 2, 2014
I did notice that the numbers seemed a bit off in terms of the area…but then saw that the number was either the x or the y and not the area…I’m sort of testing here since I don’t have a name…
Hanson - November 3, 2014
Hi,
sure test away, but you are right. I did not indicate what the Fibonacci numbers in the image refer to. Thanks for pointing that out.
Each rectangle in the figure represents a perfect square, where the number defines the length of the sides of the rectangle that surrounds the number.