Koch Island: Fractal Basics with LiveCode

Have you ever thought it would be possible to create something that had an infinitely long edge in a confined area? Yes, it is theoretically possible. Math’s is full of this kind of stuff and even thinking about the very basics of this can be great fun.

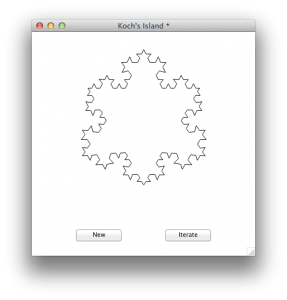
Let us consider a little island that was discovered in 1904, not by an explorer or seafarer Helge von Koch, but the Swedish mathematician with that name. This island is a mathematical idea and is considered to be one of the first fractals. It starts out as a very basic geometric construct, an equilateral triangle, which is a triangle with equal angles and equal sides. This triangle is then reshaped by dividing each line into three equally long segments and then replacing the middle segment with another equilateral triangle. The base line of that new triangle is then removed, leaving a line with a pyramid in it. The algorithm can then be applied repeatedly on the new shape, again splitting each line segment into three segments and replacing the middle one with an equilateral triangle and then removing the base line of that new triangle. After only a few iterations, it becomes apparent that the curve surrounding the island becomes increasingly longer. In fact the length of the curve increases by one third at each iteration. At the same time, the island does not appear to grow excessively and take up much more area.

Now this is all great as a mind model and we can get the principal behind the process, but what is with the infinitely long edge in the confined area that we mentioned in the beginning? Well, we could consider drawing this kind of island on a sheet of paper and think about what that would entail. From a mathematical point of view, we can represent this, we have symbols to represent infinity and the LiveCode logo has one of these infinity symbols hidden in the fifth and sixth letters, but if we really wanted to draw such an island we would have to consider what infinite really means to us in the real world.

Regardless of how fast we could replace the line segments, if it took anything longer than infinitely quick, then it would take us infinitely long to draw the island. So that is a possible showstopper. Our pen would have to be able to draw lines that are very, very thin, in fact we would have to be able to draw lines that are infinitely thin. This would then also have an impact on visibility, as lines that are infinitely thin are hard to see or measure.

These circumstances are restrictive, but it should not stop us from considering such exercises and allow us to have fun with these kind of ideas that we can partially visualize with computers. The following LiveCode scripts allows you to draw what can only be considered the tip of the iceberg of Koch island.

You can create your LiveCode Koch Island generator as follows:

1. Create a new stack.

2. Create a button “New” and place script “New” into the button script.

3. Create a button “Iterate” and place script “Iterate” into the button script.

You now have your infinitely long island curve generator that draws the first few stages of this fractal. The code is intentionally short for the blog here and shortcuts were taken in order to get here. If you want to explore this concept in more detail and see how far you can dig into the fractal, then consider updating at least the following three areas:

1. Increase the accuracy by preventing rounding from real to integer numbers at each cycle.

2. Calculate the exact height of each new pyramid with a more accurate constant. You can get the exact value by using Pythagoras.

3. Filter out duplicate point entries from “the points of graphic “island””.

Hope you have fun with this simple fractal example!

********** Script “New” **********

on mouseUp
   if there is no graphic "island" then new graphic "island"
   set the style of graphic "island" to "polygon"
    set the points of graphic "island" to "100,100" & cr & "300,100" & cr & "200,273" & cr & "100,100"
 end mouseUp

********** Script “Iterate” **********

on mouseUp
   local tLastPoint, tCurrentPoint, tCurrentIsland, tNewIsland
   put empty into tLastPoint
   put empty into tNewIsland
   put the points of graphic "island" into tCurrentIsland
   repeat for each line tCurrentPoint in tCurrentIsland
      put calculateSegment (tLastPoint, tCurrentPoint) after tNewIsland
      put tCurrentPoint into tLastPoint
   end repeat
   put line 1 of tCurrentIsland after tNewIsland
    set the points of graphic "island" to tNewIsland
end mouseUp
 
function calculateSegment pP1, pP5
   local tP2, tP3, tP4, tTran, tHeight
   if pP1 is empty then return empty
   split pP1 by comma
   split pP5 by comma
   put pP1[1] - pP5[1] into tTran[1]
   put pP1[2] - pP5[2] into tTran[2]
   put pP1[1]-tTran[1]/3 into tP2[1]
   put pP1[2]-tTran[2]/3 into tP2[2]
   put (pP1[1]-tTran[1]/2) - tTran[2]/2.886 into tP3[1]
   put (pP1[2]-tTran[2]/2) + tTran[1]/2.886 into tP3[2]
   put pP5[1]+tTran[1]/3 into tP4[1]
   put pP5[2]+tTran[2]/3 into tP4[2]
      return pP1[1] & comma & pP1[2] & cr & tP2[1] & comma & tP2[2] & cr & tP3[1] & comma & tP3[2] & cr & tP4[1] & comma & tP4[2] & cr 
end calculateSegment